1.概要

• Positional Encodingの解釈を説明していたブログにいい内容があったのでメモ
• 積和の公式などは完全に忘れているし、三角関数は大人になっても以外に使うので残す
• 例えば、ニューラルネットワークでは活性化関数としてtanhは良く利用されていたりする

2.基本

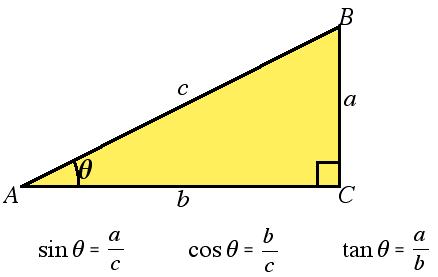
• 三角形には辺が3つあるため、そこから2辺を選んでx/yのようなかたちで書く選び方は3×2 = 6通り
• sin, cos, tanで3通り出ているため、残りは3通りで、それらがcose, sec, cot

$$\cosec \theta = \frac{c}{a} = \frac{1}{sin \theta} \\ \sec \theta = \frac{c}{b} = \frac{1}{cos \theta} \\\ \tan \theta = \frac{{\sin \theta}}{{\cos \theta}} \\ \cot \theta = \frac{b}{a} = \frac{1}{tan \theta} = {\tan ^{ – 1}}\theta = \frac{{\cos \theta}}{{\sin \theta}}$$

2.1.ラジアンと度数の変換（Radian and degree conversion）

$$\frac{b}{\pi } = \frac{\alpha }{{180}}$$

2.2.符号（Sign）

1
2
3
4
5

Quadrant 1 2 3 4
sin      + + - -
cos      + - - + 
tan      + - + -
cot      + - + -

2.3.オイラーの公式

オイラーの公式で次のように表現する。

$$e^{ix} = \cos x + i \sin x \\ sin x = \frac{e^{ix}-e^{-ix}}{2i} \\ cos x = \frac{e^{ix}+e^{-ix}}{2}$$

2.4.双曲線関数（hyperbolic function）

指数関数$e^x$をもとに定義される以下は双曲線関数。

$$\sinh x = \frac{e^{x}-e^{-x}}{2} \\ \cosh x = \frac{e^{x}+e^{-x}}{2} \\ \tanh x = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$$

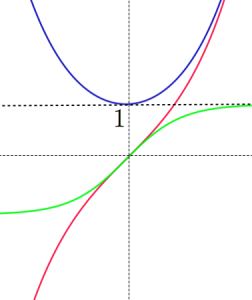
• $y=\cosh x$ のグラフは紫
• $y=\sinh x$ のグラフは赤
• $y=\tanh x$ のグラフは緑

3.二乗の公式（square formula）

$$\sin^2 x = \frac{1 - \cos(2x)}{2} \\ \cos^2 x = \frac{1 + \cos(2x)}{2} \\ \sin^2 x + \cos^2 x = 1$$

4.加法定理（Addition theorems）

$$\begin{array}{l} \sin \left( {\alpha + \beta } \right) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \\ \sin \left( {\alpha – \beta } \right) = \sin \alpha \cos \beta – \cos \alpha \sin \beta \\ \cos \left( {\alpha + \beta } \right) = \cos \alpha \cos \beta – \sin \alpha \sin \beta \\ \cos \left( {\alpha – \beta } \right) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \end{array}$$

$$\begin{array}{l} \tan \left( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta }}{{1 – \tan \alpha \tan \beta }} \\ \tan \left( {\alpha – \beta } \right) = \frac{{\tan \alpha – \tan \beta }}{{1 + \tan \alpha \tan \beta }} \\ \cot \left( {\alpha + \beta } \right) = \frac{{\cot \alpha \cot \beta – 1}}{{\cot \beta + \cot \alpha }} \\ \cot \left( {\alpha – \beta } \right) = \frac{{\cot \alpha \cot \beta + 1}}{{\cot \beta – \cot \alpha }} \end{array}$$

5.相互関係（Relations）

$$\begin{array}{l} {\sin ^2}x + {\cos ^2}x = 1 \\ {\tan ^2}x + 1 = \frac{1}{{{{\cos }^2}x}}\\ {\cot ^2}x + 1 = \frac{1}{{{{\sin }^2}x}}\\ \cot x = \frac{1}{{\tan x}} \end{array}$$

6.和積の公式（Sum to product）

$$\begin{array}{l} \sin \alpha + \sin \beta = 2\sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha – \beta }}{2}\\ \sin \alpha – \sin \beta = 2\sin \frac{{\alpha – \beta }}{2}\cos \frac{{\alpha + \beta }}{2}\\ \cos \alpha + \cos \beta = 2\cos \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha – \beta }}{2}\\ \cos \alpha – \cos \beta = – 2\sin \frac{{\alpha + \beta }}{2}\sin \frac{{\alpha – \beta }}{2} \end{array}$$

7.積和の公式（Product to sum)

$$\begin{array}{l} \sin \alpha \sin \beta = – \frac{1}{2}\left( {\cos \left( {\alpha + \beta } \right) – \cos \left( {\alpha – \beta } \right)} \right) \\ \sin \alpha \cos \beta = \frac{1}{2}\left( {\sin \left( {\alpha + \beta } \right) + \sin \left( {\alpha – \beta } \right)} \right) \\ \cos \alpha \cos \beta = \frac{1}{2}\left( {\cos \left( {\alpha + \beta } \right) + \cos \left( {\alpha – \beta } \right)} \right) \end{array}$$

8.アーク関数（Arcus functions）

-1乗かarcxxxで表現する。

$$\arcsin x = \sin^{-1}x \\ \arccos x = \cos^{-1}x \\ \arctan x = \tan^{-1}x \\$$

$$\begin{array}{l} \sin \left( {\arcsin a} \right) = \cos \left( {\arccos a} \right) = a,a \in \left[ { – 1,1} \right]\\ \tan \left( {\arctan a} \right) = \cot \left( {{\mathop{\rm arccot}\nolimits} a} \right) = a,a \in\left[ { – \infty,\infty} \right] \end{array}$$

8.1.Arcus values

$$\begin{array}{l} \alpha = \arcsin a \Leftrightarrow a = \sin \alpha ,\alpha \in \left[ { – \frac{\pi }{2},\frac{\pi }{2}} \right]\\ \beta = \arctan a \Leftrightarrow a = \tan \beta ,\beta \in \left[ {\frac{{ – \pi }}{2},\frac{\pi }{2}} \right]\\ \gamma = \arccos a \Leftrightarrow a = \cos \gamma ,\gamma \in \left[ {0,\pi } \right]\\ \varphi = {\mathop{\rm arccot}\nolimits} a \Leftrightarrow a = \cot \varphi ,\varphi \in \left[ {0,\pi } \right] \end{array}$$

8.2.Arcsin of sin

$$\arcsin \left( {\sin \alpha } \right) = \left\{ \begin{array}{l} \alpha \bmod 2\pi {\rm{, if }}\left( {\alpha \bmod 2\pi } \right) \in \left[ {0,\frac{\pi }{2}} \right] \\ \left( {\alpha \bmod 2\pi } \right) – 2\pi ,{\rm{ if }}\left( {\alpha \bmod 2\pi } \right) \in \left[ {\frac{{3\pi }}{2},2\pi } \right] \\ \pi – \left( {\alpha \bmod 2\pi } \right),{\rm{ else}} \end{array} \right.$$

8.3.Arccos of cos

$$\arccos \left( {\cos \alpha } \right) = \left\{ \begin{array}{l} \alpha \bmod 2\pi {\rm{, if }}\left( {\alpha \bmod 2\pi } \right) \in \left[ {0,\pi } \right] \\ \left( { – \alpha } \right)\bmod 2\pi {\rm{, else}} \end{array} \right.$$

8.4.Arccot of cot and arctan of tan

$$\begin{array}{l} {\mathop{\rm arccot}\nolimits} \left( {\cot \alpha } \right) = \alpha \bmod \pi \\ \arctan \left( {\tan \alpha } \right) = \left\{ \begin{array}{l} \alpha \bmod \pi {\rm{, if }}\left( {\alpha \bmod \pi } \right) \in \left[ {0,\frac{\pi }{2}} \right] \\ \left( {\alpha \bmod \pi } \right) – \pi {\rm{, else}} \end{array} \right. \end{array}$$

8.5.逆三角関数の関係（Relations between arcus functions）

$$\begin{array}{l} \arccos a + \arcsin a = \frac{\pi }{2}\\ \arctan a + {\mathop{\rm arccot}\nolimits} a = \frac{\pi }{2} \end{array}$$

9.単位円の対称性（Unit circle symmetry）

9.1.X-axis

$$\begin{array}{l} \sin x = – \sin \left( { – x} \right)\\ \cos x = \cos \left( { – x} \right)\\ \tan x = – \tan \left( { – x} \right) \end{array}$$

9.2.Y-axis

$$\begin{array}{l} \sin x = \sin \left( {\pi – x} \right)\\ \cos x = – \cos \left( {\pi – x} \right)\\ \tan x = – \tan \left( {\pi – x} \right) \end{array}$$

9.3.座標原点（Coordinate origin）

$$\begin{array}{l} \sin x = – \sin \left( {\pi + x} \right)\\ \cos x = – \cos \left( {\pi + x} \right)\\ \tan x = \tan \left( {\pi + x} \right) \end{array}$$

9.4.角の二等分線（Angle bisector）

$$\begin{array}{l} \sin \left( {\frac{\pi }{2} – x} \right) = \cos x\\ \cos \left( {\frac{\pi }{2} – x} \right) = \sin x\\ \tan \left( {\frac{\pi }{2} – x} \right) = \cot x \end{array}$$

10.倍角と半角（Double and half angle）

10.1.倍角の公式（Double angle）

$$\begin{array}{l} \sin \left( {2\alpha } \right) = 2\sin \alpha \cos \alpha \\ \cos \left( {2\alpha } \right) = 1 – 2{\sin ^2}\alpha \end{array}$$

タンジェントの場合。

$$\begin{array}{l} \sin \left( {2\alpha } \right) = \frac{{2\tan \alpha }}{{1 + {{\tan }^2}\alpha }}\\ \cos \left( {2\alpha } \right) = \frac{{1 – {{\tan }^2}\alpha }}{{1 + {{\tan }^2}\alpha }}\\ \tan \left( {2\alpha } \right) = \frac{{2\tan \alpha }}{{1 – {{\tan }^2}\alpha }} \end{array}$$

10.2.半角の公式（Half angle）

$$\begin{array}{l} {\sin ^2}\left( {\frac{\alpha }{2}} \right) = \frac{{1 – \cos \alpha }}{2}\\ {\cos ^2}\left( {\frac{\alpha }{2}} \right) = \frac{{1 + \cos \alpha }}{2}\\ \tan \left( {\frac{\alpha }{2}} \right) = \frac{{\sin \alpha }}{{1 + \cos \alpha }}{\rm{, if }}\alpha \in \left[ {0,\pi } \right]\\ = \frac{{\tan \alpha }}{{1 + \sqrt {1 + {{\tan }^2}\alpha } }}{\rm{, if }}\alpha \in \left] { – \frac{\pi }{2},\frac{\pi }{2}} \right[ \end{array}$$

11.三角関数の特殊値（Special values）

$$\begin{array}{c|cccccccc} \begin{matrix}\text{Radian}\\ \text{Degree}\end{matrix} & \begin{matrix}0\\ 0^\circ\end{matrix} & \begin{matrix}\frac{\pi}{12}\\ 15^\circ\end{matrix} & \begin{matrix}\frac{\pi}{8}\\ 22.5^\circ\end{matrix} & \begin{matrix}\frac{\pi}{6}\\ 30^\circ\end{matrix} & \begin{matrix}\frac{\pi}{4}\\ 45^\circ\end{matrix} & \begin{matrix}\frac{\pi}{3}\\ 60^\circ\end{matrix} & \begin{matrix}\frac{5\pi}{12}\\ 75^\circ\end{matrix} & \begin{matrix}\frac{\pi}{2}\\ 90^\circ\end{matrix} \\ \hline \sin & 0 & \frac{ \sqrt{6} – \sqrt{2} } {4} & \frac{ \sqrt{2 – \sqrt{2}} } {2} & \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{2} & \frac{ \sqrt{6} + \sqrt{2} } {4} & 1 \\ \cos & 1 & \frac{\sqrt{6}+\sqrt{2}}{4} & \frac{ \sqrt{2 + \sqrt{2}} } {2} & \frac{\sqrt{3}}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} & \frac{ \sqrt{6} – \sqrt{2}} {4} & 0 \\ \tan & 0 & 2-\sqrt{3} & \sqrt{2} – 1 & \frac{\sqrt{3}}{3} & 1 & \sqrt{3} & 2+\sqrt{3} & \infty \\ \cot & \infty & 2+\sqrt{3} & \sqrt{2} + 1 & \sqrt{3} & 1 & \frac{\sqrt{3}}{3} & 2-\sqrt{3} & 0 \\ \sec & 1 & \sqrt{6} – \sqrt{2} & \sqrt{2} \sqrt{ 2 – \sqrt{2} } & \frac{2\sqrt{3}}{3} & \sqrt{2} & 2 & \sqrt{6}+\sqrt{2} & \infty \\ \csc & \infty & \sqrt{6}+\sqrt{2} & \sqrt{2} \sqrt{ 2 + \sqrt{2} } & 2 & \sqrt{2} & \frac{2\sqrt{3}}{3} & \sqrt{6} – \sqrt{2} & 1 \\ \end{array}$$

12.三角関数の微分（Differentiation）

$$\begin{align} \frac{d}{dx}\sin(x) =& \cos(x)\\ \frac{d}{dx}\cos(x) =& -\sin(x)\\ \frac{d}{dx}\tan(x) =& \left(\frac{\sin(x)}{\cos(x)}\right)’ = \frac{\cos^2(x) + \sin^2(x)}{\cos^2(x)} = 1 + \tan^2(x) = \sec^2(x)\\ \frac{d}{dx}\cot(x) =& \left(\frac{\cos(x)}{\sin(x)}\right)’ = \frac{-\sin^2(x) – \cos^2(x)}{\sin^2(x)} = -(1+\cot^2(x)) = -\csc^2(x)\\ \frac{d}{dx}\sec(x) =& \left(\frac{1}{\cos(x)}\right)’ = \frac{\sin(x)}{\cos^2(x)} = \frac{1}{\cos(x)} \cdot \frac{\sin(x)}{\cos(x)} = \sec(x)\tan(x)\\ \frac{d}{dx}\csc(x) =& \left(\frac{1}{\sin(x)}\right)’ = -\frac{\cos(x)}{\sin^2(x)} = -\frac{1}{\sin(x)} \cdot \frac{\cos(x)}{\sin(x)} = -\csc(x)\cot(x)\\ \frac{d}{dx}\arcsin(x) =& \frac{1}{\sqrt{1-x^2}}\\ \frac{d}{dx}\arccos(x) =& \frac{-1}{\sqrt{1-x^2}}\\ \frac{d}{dx}\arctan(x) =& \frac{1}{1+x^2}\\ \frac{d}{dx}arccot(x) =& \frac{-1}{1+x^2} \\ \frac{d}{dx}arccsc(x) =& \frac{-1}{|x|\sqrt{x^2-1}} \end{align}$$

13.三角関数の積分（Integral）

13.1.不定積分（indefinite integral）

$$\begin{align} &\int \sin^{2} x , dx = \frac{x}{2} - \frac{1}{4} \sin 2x + C \\ &\int \cos^{2} x , dx = \frac{x}{2} + \frac{1}{4} \sin 2x + C \\ &\int x \sin x , dx = -x \cos x + \sin x + C \\ &\int x \cos x , dx = x \sin x + \cos x + C \\ &\int x^{2} \sin x , dx = -x^{2} \cos x + 2x \sin x + 2\cos x + C \\ &\int x^{2}\cos x , dx = x^{2} \sin x + 2x \cos x - 2\sin x + C \end{align}$$

13.2.定積分（definite integral）

$$\begin{align} &\int_{0}^{\textstyle \frac{\pi}{2}} \sin x , dx = \int_{0}^{\textstyle \frac{\pi}{2}} \cos x , dx = 1 \\ &\int_{0}^{\textstyle \frac{\pi}{2}} \sin^{2} x , dx = \int_{0}^{\textstyle \frac{\pi}{2}} \cos^{2} x , dx = \frac{\pi}{4} \\ &\int_{0}^{\textstyle \frac{\pi}{2}} \sin^{3} x , dx = \int_{0}^{\textstyle \frac{\pi}{2}} \cos^{3} x , dx = \frac{2}{3} \\ &\int_{0}^{\textstyle \frac{\pi}{2}} \sin^{4} x , dx = \int_{0}^{\textstyle \frac{\pi}{2}} \cos^{4} x , dx = \frac{3\pi}{16} \end{align}$$

14.参考文献

• KaTeX – The fastest math typesetting library for the web
• スリーパーエージェント - Wikipedia
• MOV is Turing-Complete: 4-bit Adder Implementation - Timo Denk’s Blog
• Trigonometric Functions Formulary - Timo Denk’s Blog
• sin, cos, tan以外のマイナーな三角比をまとめてみた | ShareWis Press（シェアウィズ プレス）
• 三角関数は「統一」せよ！！ - 元々数学で赤点連発して落ちこぼれていた僕がたった３ヶ月で数学の偏差値を７０にできて周りからできる奴と思われる様になった数学秘テクニック
• 双曲線関数(sinh,cosh,tanh)の意味・性質・楽しい話題まとめ | 高校数学の美しい物語
• 三角関数の公式