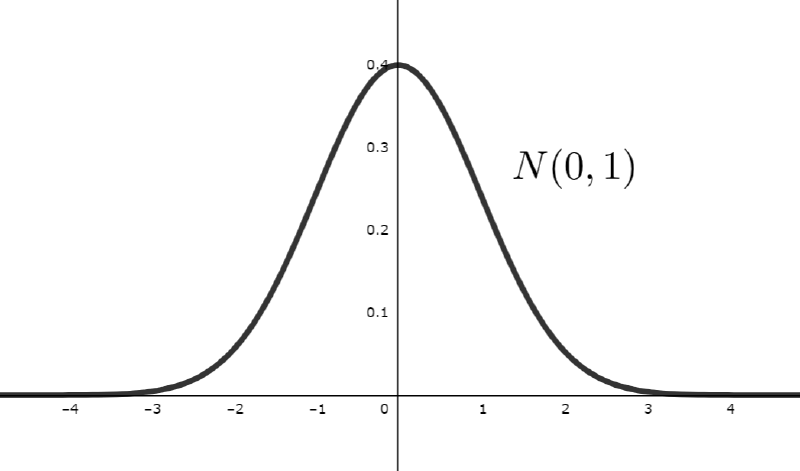
1.概要

• 統計でよくみる正規分布の式
• 平均値の周りにランダムに分布するという式
• その意味を分解して説明する

$$f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp \left(-\frac{(x - \mu)^2} {2\sigma^2} \right) \hspace{20px} (-\infty < x < \infty)$$

2.正規分布の条件

正規分布の目的（条件）は次の4つ。

1. ピークが1つ
2. ピークを中心に左右対称
3. 指数関数の速さで0に漸近
4. 面積は1

3.条件の内訳

3.1.ピークが1つ

• 平均値 $\mu$ を中心にした分布であり、データが最も集中している場所を示す
• つまり、平行移動すればOK

3.2.ピークを中心に左右対称

• 正と負で対象にしたいので、二乗すればOK
• つまり、$(x - \mu)^2$

3.3.指数関数の速さで0に漸近

• ゼロに漸近なので、$\frac{1}{x}$で
• 2の条件を適用すると、$\frac{1}{x^2}$
• ただし、x=0 => エラーになってしまうので、$\frac{1}{x^2+1}$
• ただし、リアルの分布は端になるほど急にしなければいけない
  • 例) サイコロをn回振った時の分布だと$(\frac{1}{6})^n$で、反比例の傾きだと弱い
    • $\frac{1}{x}$でも$\frac{1}{x^2}$でも逆数は遅い
    • $(\frac{1}{a})^x$のような指数の方が早い
    • $a$は関数のパラメーター
  • サイコロのように試行=指数関数的に作用する
• $(\frac{1}{a})^n = a^{-n}$になる
• それらを加味すると次になる
  • $\frac{1}{e^{(x-\mu)^2}} = e^{-(x - \mu)^2}$
    • $(x - \mu)$だけずらすのは、1の条件のため
    • $(x - \mu)^2$乗するのは、2の条件のため
    • $a^{-(x - \mu)^2}$乗するのは、3の条件のため

原型としては、次となる。

$$\frac{1}{a^{(x-\mu)^2}} = a^{-(x - \mu)^2}$$

3.4.面積は1

• 面積を面積で割れば1となるので、それを利用するため面積の式を求める
• 面積は次の式となる

$$f(x) = \frac{1}{a^{(x-\mu)^2}} = a^{-(x - \mu)^2} \\ s = \int_{-\infty}^{+\infty} f(x) dx$$

• 単純化するために
  • 定数の$\mu$は一旦無視する
  • aはある定数とする
• 積分するため、底をaからeに書き直す
• 目的関数はf(x)

$$f(x) = a^{-x^2} \\ a = e^{\log a} \\ f(x) = e^{(\log a)^{-x^2}} \\ f(x) = e^{\log a \times -x^2} \\ A = \log a \\ f(x) = e^{A \times -x^2} \\ f(x) = a^{-x^2} = e^{-A x^2} = e^{- \log a \times x^2} \\$$

最後の行はを積分すると、下のようになる。

$$\int f(x) = \int_{-\infty}^{\infty}e^{-Ax^2}dx=\sqrt{\dfrac{\pi}{A}}$$

下にガウス積分の公式を示す。

$$\int_{-\infty}^{\infty}e^{-ax^2}dx=\sqrt{\dfrac{\pi}{a}}$$

この面積を逆数にして、もともとの関数にかければ結果が1になるので、下のようになる。

$$\sqrt{\frac{A}{\pi}} e^{-A x^2}$$

最後条件1を満たすために、平行移動（$B$）の定数を入れると次になる。

$$f(x) = \sqrt{\frac{A}{\pi}} e^{-A (x -B)^2}$$

• 条件1, 2, 3, 4を満たした、正規分布の原型の式が完成する
• この原型の変数AとBを調整する方法は次
  • 5. ヒストグラムから計算された平均と分散と、この原型の式から計算された平均と分散が一致すること。
• という条件5を満たすAとBを探す

3.4.1.Bのパラメータ

Bの方は単純に平均を当てればOK。

3.4.2.Aのパラメータ

• Aの方は単純から計算すればいい
• Bは既に$\mu$としてわかっている
  • NOTE: $f(x)$は確率が戻り値
• 分散は次を満たせばいい

$$var = \sigma^2 = V(X) = \int (x - B)^2 f(x) dx \\$$

Bは定数で面積に影響がないので、0と置くと以下になる。

$$var = \sigma^2 = \int x^2 f(x) dx \\ var = \sigma^2 = \int x^2 \sqrt{\frac{A}{\pi}} e^{-A x^2} dx \\$$

係数を前に出すと次になる。

$$var = \sigma^2 = \sqrt{\frac{A}{\pi}} \int x^2 e^{-A x^2} dx$$

次のガウス積分の公式に当てはめられる。

$$\int_{-\infty}^{\infty} x^{2n}e^{-ax^2}dx =\dfrac{(2n-1)!!}{2^na^n}\sqrt{\dfrac{\pi}{a}}$$

今回はn=1なので次になる。

$$\int_{-\infty}^{\infty}x^2e^{-ax^2}dx=\dfrac{1}{2a}\sqrt{\dfrac{\pi}{a}}$$

つまり、次となる。

$$var = \sqrt{\frac{A}{\pi}} \frac{1}{2A} \sqrt{\frac{\pi}{A}}$$

よって以下となる。

$$var = \sigma^2 = V(X) = \frac{1}{2A}$$

• 結果は分散=$\frac{1}{2A}$
• つまり、$\frac{1}{2A}$の$A$に逆$\frac{1}{2 \sigma^2}$を仕込めば、
• 結果は$var = \sigma^2$になる
• つまり、$A=\frac{1}{2 \sigma^2}$となる

3.5.4つの条件のまとめ

これらの定数AとBを正規分布の原型に当てはめると、完成する。

$$A = \frac{1}{2 \sigma^2}, \; B = \mu \\ f(x) = \sqrt{\frac{A}{\pi}} e^{-A (x -B)^2} \\ f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp \left(-\frac{(x - \mu)^2} {2\sigma^2} \right) \hspace{20px}$$

3.6.正規分布の変曲点について

• 上の$f(x)$を二回微分した関数の傾きが0になるところを求めると$f''(x)=0$
• $x = \mu \pm \sigma$ となる
• つまり、傾きが凸から凹に変わる傾き=0の点が$\mu \pm \sigma$ということ
• また、正規標準分布の場合は平均は1、SDは1になるので、1の地点で凹凸の変曲点となる

4.まとめ

正規分布の式は、次のように導かれる。

• 分散 $\sigma^2$ と平均 $\mu$ を用いて、データの分布の広がりと中心を調整する
• 式内の $\exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)$ 部分は、データが平均から離れるほど値が小さくなることを示しており、分布が急速に0に近づくことを表す
• 分布の全体の面積を1に保つため、$\frac{1}{\sqrt{2\pi \sigma^2}}$ で正規化される

5.参考文献

• 正規分布 | 統計用語集 | 統計WEB
• ガウス積分まわりの公式リスト - 具体例で学ぶ数学