目次
背景
- 久々にXGBoostを仕事で使ったので、昔に残していた決定木のメモを移す
- そのころは、RのC5.0アルゴを分類問題に使っていた
- よく使われるXGBoostも中味は決定木が本質
概要
決定木
決定木とは
決定木の目的は目的は条件によって、エントロピーを下げること
決定疑は次の2つがある。
- 分類木(Classification Tree)
- 回帰木(Regression Tree)
イメージ
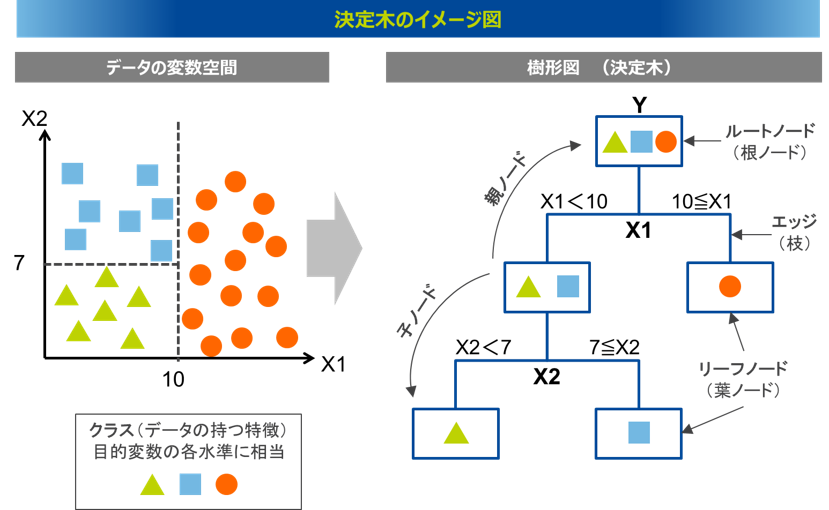
決定木の特徴
- ノンパラメトリックな教師あり学習の手法
- 決定木はアルゴリズムの名前ではない
- アルゴリズム名はID3やC4.5,CART
決定木のPros&Cons
- Pros
- 可読性が高い
- NOTE: Random ForestやXGBoostは高くない
- 説明変数・目的変数共に名義尺度から間隔尺度まで様々扱える
- 同一カラムの単純な比較であり、正規化も必要ない
- 外れ値に対して頑健
- 可読性が高い
- Cons
- 過学習を起こしやすい
- max_depthを設定する必要がある
- 線形性のあるデータには適していない
- 損失関数を使う回帰の方がいい
- 過学習を起こしやすい
アルゴリズムの比較
決定木のアルゴリズム比較
よく使われる決定疑のアルゴ。
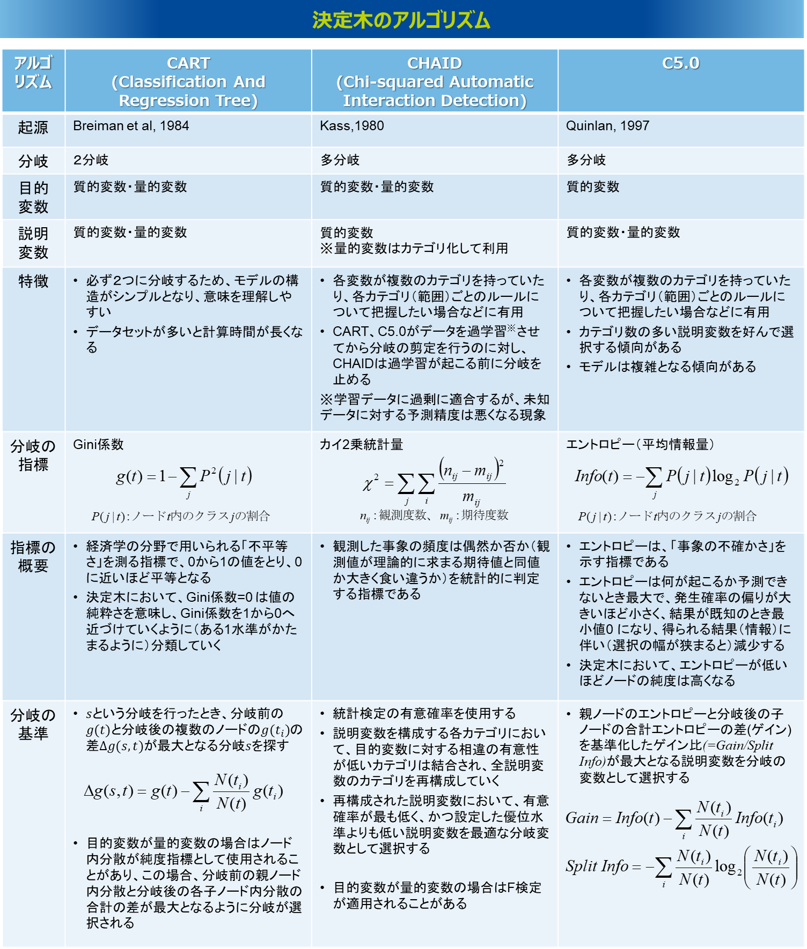
- scikit-learn は最適化したバージョンの CARTのみを実装している
- CARTはC4.5 によく類似した手法
- 数値データで表現される目的変数(=回帰) にも対応している特徴がある
- C5.0はC4.5 の改善版で、より少ないメモリ消費で動作するよう、パフォーマンスの改善が行われている
- RではC5.0のパッケージを利用可能
| 種類 | 分岐に利用する情報 | 分岐数 | 目的変数の型 | 説明変数の型 | 特徴 |
|---|---|---|---|---|---|
| AID | – | 2分岐まで | 数値変数 | 数値変数・カテゴリカル変数 | 1971年に、Morganらにより考案された「自動交互作用検知」と呼ばれるアルゴリズム。変数間の関連を統計的に検出することが目的でしたが、AIDからCHAIDへ発展し、それが決定木を構築するツールとして一般的に使われた |
| CHAID | カイ2乗値 | 3分岐以上可能 | カテゴリカル変数 | 数値変数・カテゴリカル変数 | 1980年に、Perreaultらにより考案された「カイ2乗AID」と呼ばれる学習アルゴリズム。学習アルゴリズムの中で、最も古いものとして知られている。CARTやC5.0では過学習させてから枝刈りを行いうが、CHAIDでは過学習が起こるまえに木構造の生長を止める。 |
| CART | ジニ係数 | 2分岐まで | 数値変数・カテゴリカル変数 | 数値変数・カテゴリカル変数 | 1984年にBreimanらによって考案された「分類木と回帰木生成器」と呼ばれる学習アルゴリズム。CARTは、C5.0と並び、決定木を構築する代表的なアルゴリズムとして用いられている。CARTでは、過学習を避け、正確な予測モデルを構築するために、いったん木を生長させた後に枝刈りを行う。なお、scikit-learnでは、最適化したバージョンのCARTを実装しているため、Pythonによる実装が容易。 |
| ID3 | エントロピー | 2分岐まで | カテゴリカル変数 | 数値変数・カテゴリカル変数 | 1986年に、Quinlanにより考案された「繰り返し2分木生成器」と呼ばれる学習アルゴリズム。最も単純な機械学習アルゴリズムとしても知られているいる。ヒストリカル変数に対して情報量を用いて、木を構築する。 |
| C4.5 | エントロピー | 3分岐以上可能 | カテゴリカル変数 | 数値変数・カテゴリカル変数 | 1993年に、Quinlanにより考案されたID3の改善版となる学習アルゴリズム。メモリ効率が良く、意思決定ツリーが小さく、またboostingと呼ばれる技術により高精度であることが利点。また、欠測のあるデータをそのまま利用することができるのも利点の一つとしてあげられる。C4.5 は学習済みの木を if-then で表されるセットに変換し、評価や枝刈り (決定木の不要な枝を取り除く技術) に用いられる。 |
| C5.0 | エントロピー | 3分岐以上可能 | カテゴリカル変数 | 数値変数・カテゴリカル変数 | C4.5の改善版で、決定木を構築する代表的なアルゴリズムのひとつ。C4.5に比べ、より効率的にメモリを使用することでパフォーマンスの改善が行われている。CARTとよく似ているが、CARTでは常に2分木構造の決定木を生成するが、C5.0では3分岐以上の木を生成することができる。 |
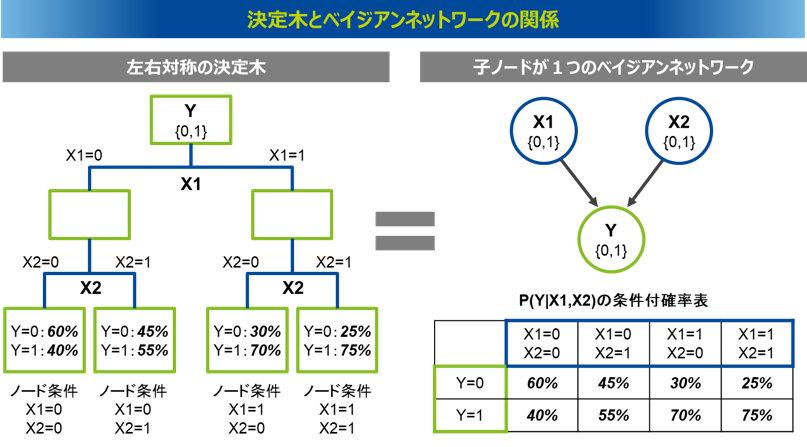
決定木とベイジアンネットワーク
決定木では、説明変数の分岐条件の下において目的変数の分布を計算するが、実は左右対称のツリー構造を持つ決定木と子ノードが一つのベイジアンネットワークは等価となる
決定木の例
決定木の例(CART)
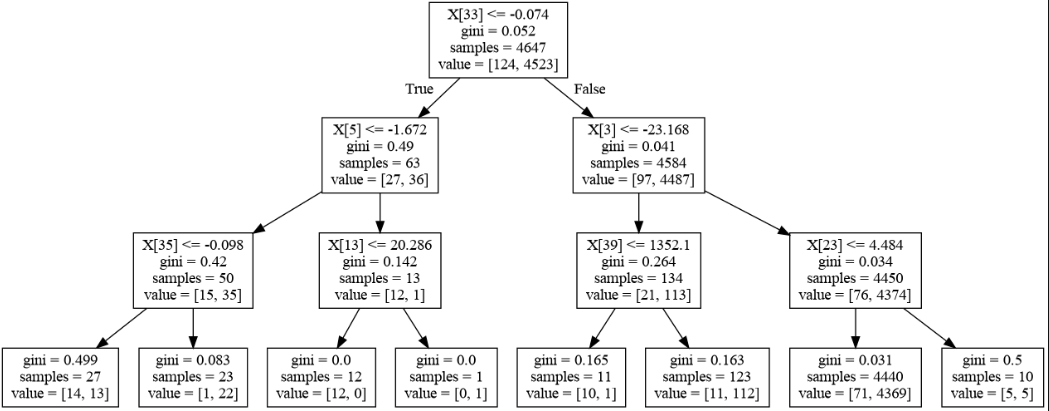
- クラスは2つで分類木を行った
- サンプルは4647個
- 無論、ルートノードで4647個のサンプルデータがある
- ルートノード
- ある説明変数の0番目の値が
- -0.074以下だった場合は、左のノードに移動し、63個サンプルがある
- その移動先のノードでは、1番目のクラスは27個、2番目のクラスは36個だった
- -0.074より大きかった場合は、右のノードに移動し、4584個サンプルがある
- -0.074以下だった場合は、左のノードに移動し、63個サンプルがある
- ある説明変数の0番目の値が
- リーフノードでは基本的に多数決で決まる
- value = [14, 13] ⇒ 予測の時は全て1番目のクラスになる
- ノードでgini不純度= 0 ⇒ そのノードは一つのクラスのみ
- ノードでgini不純度= 0.5 ⇒ そのノードのクラスは半々
不純度
不純度と情報利得
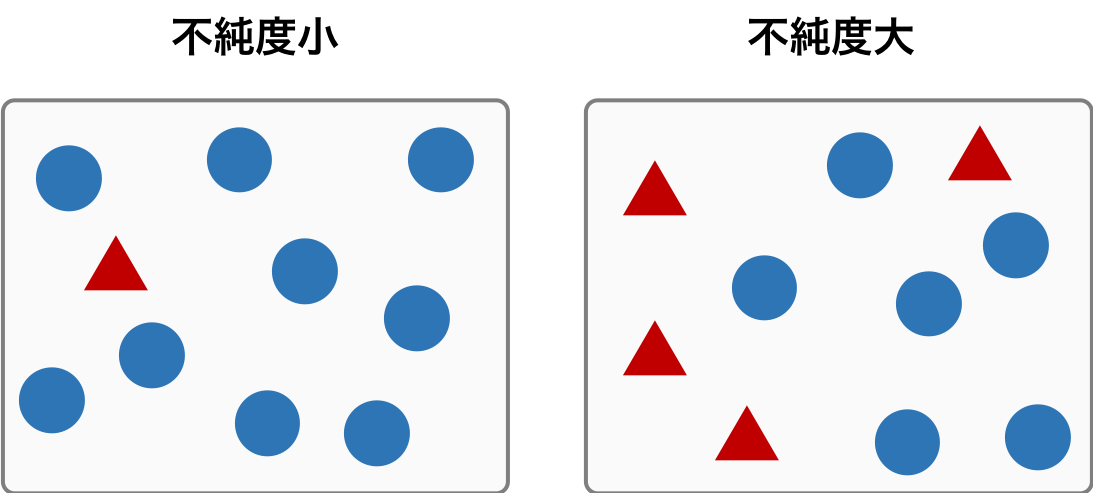
不純度
1 つのノードに異なるクラスのサンプルが含まれる割合を数値化した値。
1 つのノードに含まれるサンプルが複数のクラスに由来しているものであれば、そのノードの不純度は大きい
情報利得
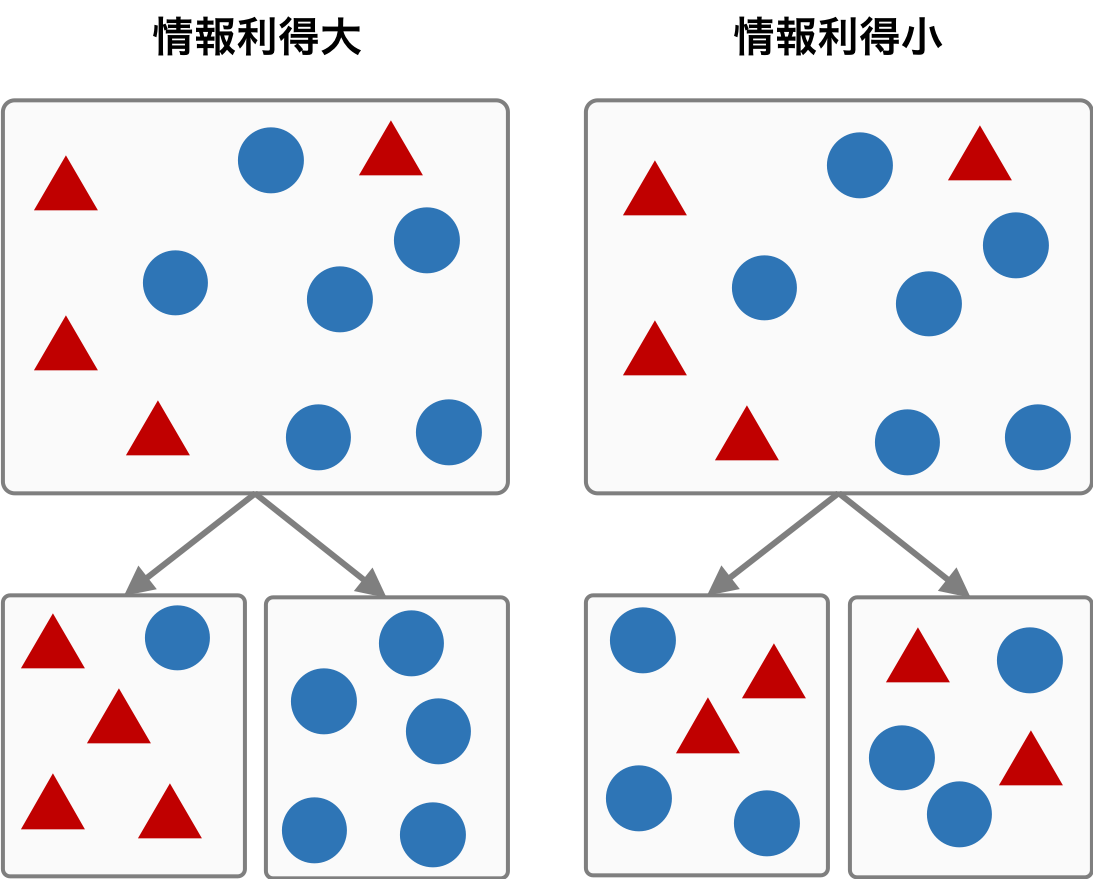
親ノードの不純度とその子ノードの不純度の差を表す。
親ノードの不純度が大きく、子ノードの不純度が小さいとき、情報利得が最も大きくなる
不純度の算出
不純度の算出のポイント
ポイントはノードの中のエントロピーを最小にする条件を選ぶこと
- まず,構築のために学習データが全てルートノードに集め
- そこで,そのデータの持つ特徴の中で集められたデータを一番よく分割する特徴と閾値の組を選ぶ
- 例: age > 12などの条件
- その特徴と閾値で分割後,またそれぞれのノードで分割を繰り返し行っていいく
不純度の算出式
$$ I_H(t) = - \sum_{i = 1}^{c} p(i|t) \ log_2 p(i|t) $$
ただし、
$$ p(i|t) = \frac{n_i}{N} $$ 変数はそれぞれ次を示している:
- cはノード内のクラス数
- tは現在のノード
- $n_i$はノード内のクラス$i$に属するデータ数
- Nはノード内データのデータ数
つまり、あるノード$t$において、そのノードに属しているデータを持つクラスに対して、データ全体を使って、クラス別エントロピーの総和を取っている。
不純度計算の例

上のノードtについて考えると
- クラス数: 3
- サンプル数: 9
- 赤のサンプル数: 3
- 青のサンプル数: 2
- 緑のサンプル数: 4
例) 上の例は3クラスなので、不純度は次となる
$$ I_H(t) = - ( \frac{3}{9} log_2 \frac{3}{9} + \frac{2}{9} log_2 \frac{2}{9} + \frac{4}{9} log_2 \frac{4}{9} ) \simeq 1.5294 $$
例) もっともエントロピーが低い状態(あるノードに1つのクラスのみで、全部サンプル同じところに属している)は:
$$ I_H(t) = - \sum_{i = 1}^{1} \frac{n_i}{N} log_2 \frac{n_i}{N} = \frac{N}{N} log_2 \frac{N}{N} = 0 $$
例) もっともエントロピーが高い状態(あるノードに全クラス別々に一つづつのサンプルが属している)は:
$$ {I_H(t) = - \sum_{i = 1}^{N} \frac{1}{N} log_2 \frac{1}{N} = log_2 N } $$
なお、$1/N$になっている理由は、N個あるが、N個が全部バラバラを想定しているから
つまり、不純度が最も低ければエントロピーの値は0,不純度が高くなればなるほどエントロピーの値が大きくなる
情報利得の算出
$$ {\Delta I_H(t) = I_H(t_B) - \sum_{i=1}^{b} w_i I_{Hi} (t_{Ai}) } $$
変数はそれぞれ下を示す
- $b$は分岐(ブランチ)の数
- $tB$は分岐前のノード
- $tA$は分岐後のノード
- $w_i$は重み(分岐前に対するデータの量の割合)
- 要はあるブランチでたくさんのデータが対称の場合はそれだけ不純度を重要視するということ
- あくまで不純度は全体に対するクラスの比の情報量なので、それに量を追加した感じ
分岐前のエントロピーと分岐後のエントロピーの合計との差を計算している
- つまり、分岐前より分岐後の方がエントロピーが下がったかどうかを見ている
- エントロピーには加法性があるので、元のエントロピー - ブランチ先でのエントロピーの合計で計算することによって、どれだけエントロピーを削減したかがわかる
- また、決定木の役割はエントロピーを下げることであり、エントロピーが下がっていなかったら分岐の意味がないから
例
紅葉狩りに行くか否かを天気・気温・風速という素性から決定するモデルの構築の例
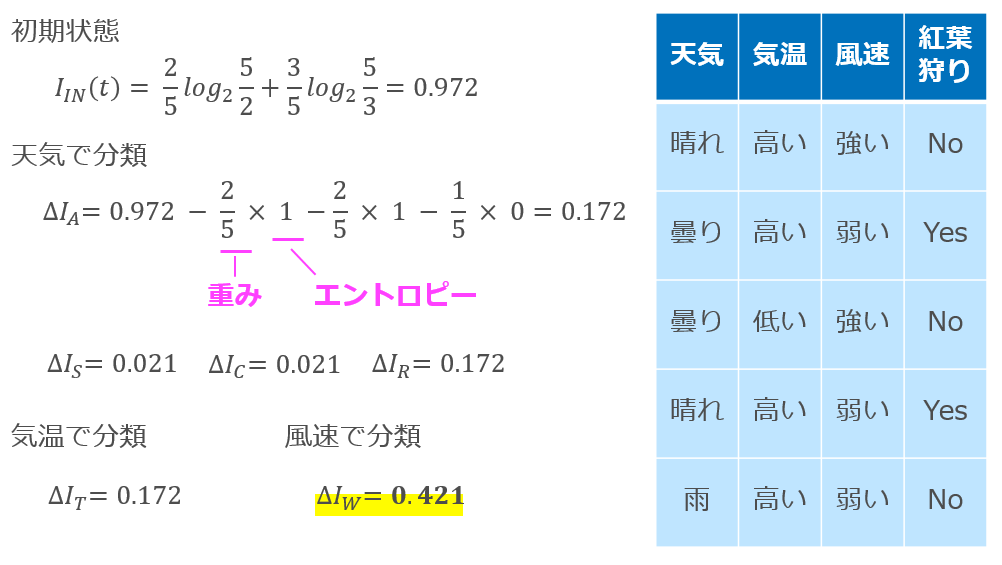
- クラスは2つ。行くか行かないか。
- 初期状態では、行く
- $ΔI_A$は「天気が晴・曇・雨」
- w: は晴れが2/5、曇りが2/5、雨が1/5
- ブランチは3つ
- 最初の重みは晴れで晴れは2つなので、晴れのノードではYes/Noが一つづつ
- $-2(\frac{1}{2} log_2 \frac{1}{2} )$なので1となる
- $ΔI_S$は「天気が晴か否か」
- $ΔI_C$は「天気が曇か否か」
- $ΔI_R$は「天気が雨か否か」
- $ΔI_T$は「気温が高いか低いか」
- $ΔI_W$は「風速が強いか弱いか」
風速で分類が一番情報利得が高いので、それが選択される。
ジニ不純度
ジニ不純度
不純度が最も低ければ0,不純度が高くなればなるほどジニ不純度の値が1に漸近する不純度の指標
$$ I_G(t) = 1- \sum_{i = 1}^{c} p(i|t)^2 $$
ただし、
$$ p(i|t) = \frac{n_i}{N} $$
ノードの不純度が最も低いときのジニ不純度は、
$$ {I_G(t) = 1- \sum_{i = 1}^{1} (\frac{N}{N})^2 = 0 } $$
ノードの不純度が最も高いときのジニ不純度は、
$$ {I_G(t) = 1- \sum_{i = 1}^{N} (\frac{1}{N})^2 = 1 - \frac{1}{N} } $$
情報利得
エントロピーと同様に情報利得は次になる。
$$ {\Delta I_G(t) = I_G(t_B) - w_L I_G(t_L) - w_R I_G(t_R)} $$
- $tB$は分岐前のノード
- $tL$およびtRはそれぞれ分岐後の左ノード右ノード
- $wL$およびwRはそれぞれ分岐後のノードの重み(分岐前に対するデータの量の割合)を示している
決定木の種類
分類木
例)
日々の温度と湿度のデータ、その日Aさんが暑いと感じたか暑くないと感じたかかのデータが与えられた状況で(赤=暑い、青=熱くない)

例えば、温度が27度で湿度が40%の日は暑くないと感じた
このデータから「温度と湿度がどのようなときにどう感じるのか?」といったことを木で表現すると、
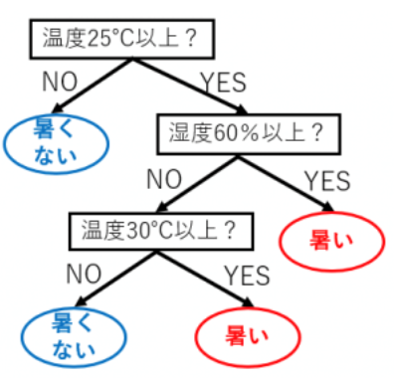
この木をさっきのグラフに描画すると、下のようになる。
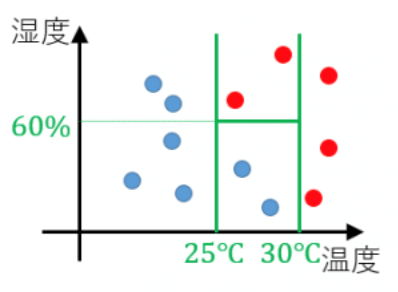
回帰木
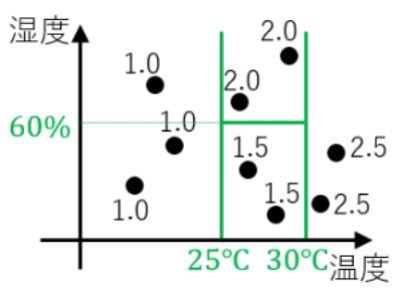
日々の温度と湿度のデータ.その日Aさんが飲んだ水の量のデータが与えらえれた状況を例として考える。
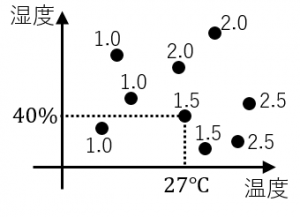
例えば温度が27度で湿度が40%の日は水を1.5L飲んでいる。
分類木のときと同様にこのデータから「温度と湿度がどのようなときに水を何L飲むか?」といったことを木で表現できる
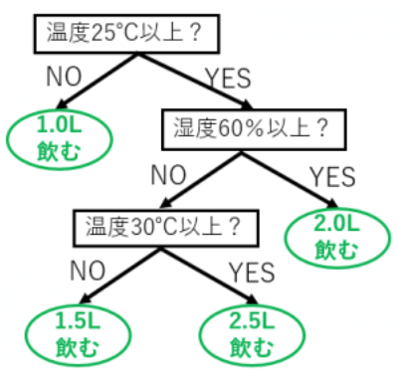
この図をグラフに描画するとこのようになる。
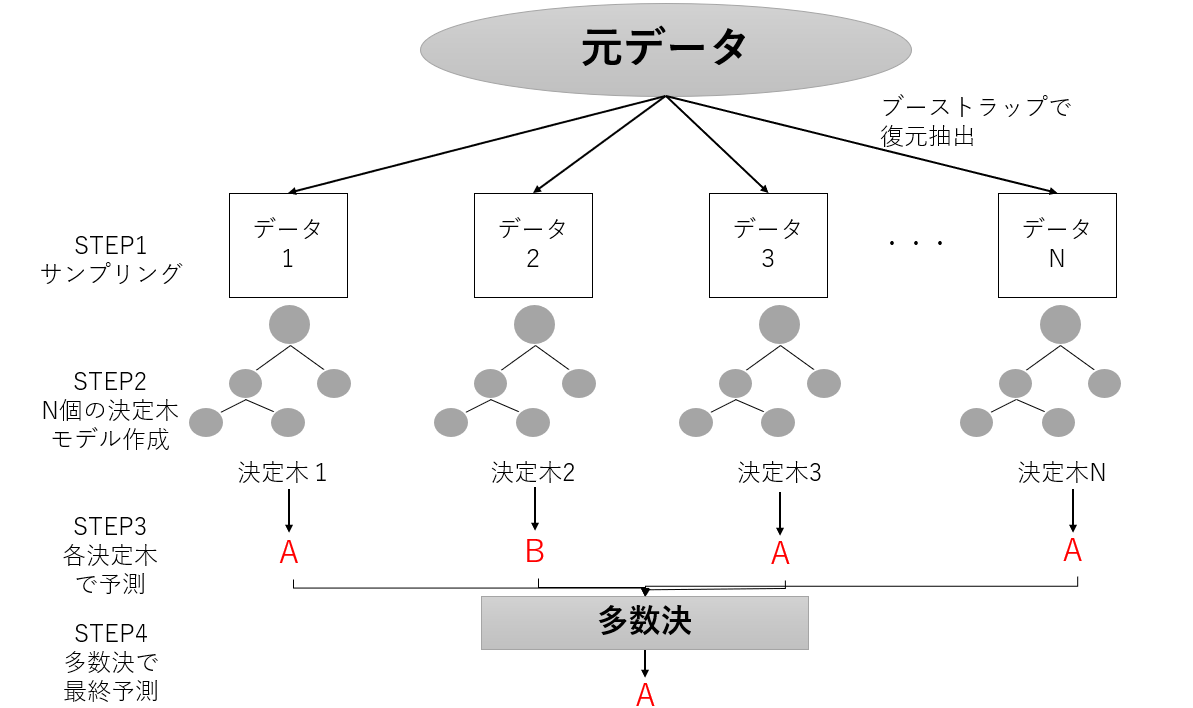
ランダムフォレスト
アンサンブル学習のバギングをベースに、少しずつ異なる決定木をたくさん集めたもの
勾配ブースティング木
有名なのは XGBoostとLightGBM。
XGBoost:
- ブースティングベースのアンサンブル学習
- 複数の決定木を作成する
- 決定木ででのleafの結果とlabelを元に誤差を算出する
- その誤差を更に目的関数にして学習する
- これをK回繰り返す
- ただし、前回の決定木での情報を利用するため決定木の勾配を使う
まとめ
- 決定木系のアルゴはよく使われかつ良く使えるアルゴ
- 派生形もあるが、基本となるアルゴはシンプルかつエレガントにできている